كيف يعمل القمر الصناعي نظريا

لنتخيل مرة ثالثة أن هذه القذيفة تجذبها قوة إلى الأرض وهي قوة الجاذبية في حين تدفعها قوة أخرى نحو الخارج، حيث تتساوى القوتين مع إضافة عدم وجود إحتكاك، هنا ستتخذ القذيفة مدارا حول الأرض وستسير بشكل لانهائي من خلال الدفع الأول أو السرعة الإبتدائية مع التنبيه إلى أننا نفرض أن الجاذبية متساوية بشكل كامل فوق كل الكوكب. والشكل التالي سيوضح لك كيف ستسير القذيفة:
لنتخيل الآن أن تلك القذيفة هي قمر صناعي، قمنا برميه من الفضاء وبدون وجود إحتكاك ووجود قوتين متعاكستين الأولى تجذبه إلى الأرض والثانية تدفعه هنا ستلاحظ أن القمر سيدخل في مسار لانهائي ويبقى يسير بدون الحاجة إلى أي دافعات. هذه هي فلسفة السير بدون دافعات ويسميها البعض بالسقوط الدائم للقمر الصناعي ولكن بدون سقوط. فيما يلي سأقوم بتوضيح ذلك من خلال الفيزياء، أي سنثبت وجود هذه الأفكار على أرض الواقع بشكل نظري وهو أول ما يجعلك تربط بين عدة أشياء وهي الفلسفة والعلم مماثل بالفيزياء والرياضيات كلغة للعلم والتكنولوجيا وهي القمر الصناعي وهو ما يجعلك منبهرا بقدرة الرياضيات والفيزياء على صنع أشياء مميزة جدا وقدرة علماء مثل نيوتن على صياغة قوانين جعلتنا نقفز خطوات كبيرة نحو الأمام، نحو المعرفة، ونحو حدود جديدة للعقل.
كيف يعمل القمر الصناعي فيزيائيا
في هذا الجزء سنقوم بدراسة حركة القمر الصناعي فيزيائيا لذلك ستجد هنا مجموعة من النظريات والقوانين التي تم تبسيطها ليفهمها أي شخص كان, القوى المذكورة هنا مهمة لدراسة حركة القمر الصناعي, لذلك ستجد في الأخير خلاصة العمل الذي قمنا به.. لنبدأ
في حركة القمر الصناعي توجد العديد من القوى المؤثرة عليه وهذه القوى هي كالآتي :
- الجاذبية الأرضية.
- قوة الطرد المركزي.
- قوة الإحتكاك
- قوة الدفع
1- الجاذبية الأرضية
هي ما نعني به ميل الأجسام للإتجاه نحو الأرض في حالة دخولها في مجال الجاذبية، والجاذبية بشكل عام نقصد بها ميل الأجسام إلى الإتجاه إلى بعضها البعض وتم صياغة قانون الجاذبية العام من قبل العالم نيوتن حيث قام بربط الكتلة وثابت الجذب العام لكيبلر والمسافة بين الجسمين وهو كما يلي:

القوة الناتجة عن الجاذبية F
ثابت الجذب العام ويساوي في تقدير النظام القياسي G
كتلة الأرض M
كتلة الجسم الذي نريد قياس قوة الجاذبية عنده مثال القمر الصناعي m
البعد بين الجسمين ( بين مركزيهما ) d
يجب أن تعرف هذا القانون جيدا لكي نستخدمه فيما بعد في ربط الحلقات بين القوة الطاردة المركزية والجاذبية الأرضية.
قوة الطرد المركزي هي قوة غير حقيقية ولكن يمكننا القول على أنها ناتجة عن أن الأجسام تميل للسير في خط مستقيم وفي حالة جسم يدور في مسار دائري فهو في كل مرة يميل للخروج عن مساره ولكن القوة الجاذبة المركزية ( في حالة قمر صناعي هي الجاذبية األرضية ) تمنعه عن الخروج وهنا نقول أن الدفع للخارج ال توجد قوة تسببه فهو نتاج عن العطالة الذاتية لألجسام ( السير في خط مستقيم بسرعة ثابتة تسمى العطالة الذاتية ).
ربما الصصورة التالية توضح لكم الأمر بشكل جيد:
ونلاحظ هنا أن هناك ثلاث أشياء تأثر على قوة الطرد المركزي هي نصف قطر الدوران وسرعة الجسم وكتلته وهي ثلاث متغيرات فقط تدخل في بناء معادلة قوة الطرد المركزي وهي كالتالي:
قوة الطرد المركزي F
كتلة الجسم m
سرعة الجسم v
نصف قطر الدوران R
قوة الإحتكاك هي قوة معاكسة للقوة المحركة وتعمل على تقليل سرعة الأجسام، وهي ناتجة عن تلامس بين جسمين، على الأرض يعمل الهواء على إعاقة حركة الطائرات من خلال الإحتكاك بهيكل الطائرة وفي نفس الوقت هو عنصر مهم في طيرانها لأنه بدون إحتكاك بالهواء لا يمكن للطائرة أن تطير. وعلي تقديم ملاحظة هنا وهي أن القوة المحركة هي قوة تجعل الشيء يتحرك قد تكون دفعا أوليا أو محركا أو دافعات نفاثة.
في الفضاء يوجد الفراغ، ما نعني بالفراغ هو عدم وجود غازات ولكن لكي نتحدث بشكل دقيقة يوجد القليل جدا من الغازات حيث نسبتها تقترب من الصفر ولكن عموما ولأننا نحب التقريب فإننا نقول أنه لا يوجد غازات في الفضاء لأنها بالطبع هي مأثرة على المدى الطويل جدا، فننطلق من هذا ونقول أنه لا يوجد إحتكاك في الفضاء وهذا شيء مهم جدا لأن الإحتكاك كما قلت سابقا يمنع على تقليل سرعة الأجسام وإعاقة مسارها وهو ما يجعلنا نحتاج لقوة محركة في كل مرة لدفع الأجسام ولكن في الفضاء لا يوجد هذا فأنت إذا دفعت الجسم لن يتوقف عن الدوران وهو ما تحدثت عنه في قصة المدفع أين عندما قذفنا القذيفة وبدون وجود إحتكاك لم تتوقف عن إكمال مسارها ( نحن نسمى الغازات بالهواء بالشكل العام ) لذلك نقول أن الهواء على الأرض هو ما يسبب الإحتكاك مع الأجسام الطائرة وبكل ما يحمله ذلك الهواء فنحن إما سنستفيد منه مثال في إقلاع الطائرة بشكل إيجابي أو سيأثر علينا بشكل سلبي في حالة أننا نريد رمي شيء في الفضاء ولا نريده أن يتوقف لذلك في الفضاء لا يوجد هواء وهذا ما يدفعنا إلى أن نقول أنه لا يوجد إحتكاك.
القوة المعيقة للقمر الصناعي أو قوة اإلحتكاك B
قوة الطرد المركزي A
قوة الجاذبية الأرضية P
فنكتب الآن محصلة القوى المؤثرة على القمر الصناعي من خلال قانون نيوتن الثاني:
من أجل أن يسير القمر إنطلاقا من سرعة إبتدائية وبدون توقف نحن نحتاج إلى أن تبقى فقط القوة المحركة، وهذا يكون من خلال أن الإحتكاك يجب أن يكون معدوما
وكذلك بالنسبة للجاذبية الأرضية وقوة الطرد المركزي. في الفضاء الإحتكاك معدوم وسبق توضيح ذلك ويتبقى لنا فقط الجاذبية وقوة الطرد المركزي التي لا يمكن أن يكونا معدومين ولكن كما نلاحظ فهما متعاكسين في الإتجاه إذن يمكن أن يكونا متساويين ومنه ولأنهما متعاكسين نستطيع الوصول إلى إعدامهما معا ومنه ستبقى لنا فقط القوة المحركة. إذن هدفنا التالي هو إيجاد شرط يكون تكون فيه الجاذبية والقوة الطاردة المركزية متساويتين ومنه نستطيع تثبيت هذا الشرط للحصول على قمر صناعي يسير بدون دوافع.
في المحور السابق أنهيت بأنه علينا أن نجعل قوة الدفع المركزي وقوة الجاذبية متسوايتين ولذلك من أجل أن يسير القمر الصناعي بشكل لا نهائي بدون محرك فقط من خلال سرعة إبتدائية وقلت تحديدا أنه علينا البحث عن شرط نتحكم به لنحقق الفكرة. إذن ما أقصده بالتساوي هو هذه المتطابقة :
وإذا قمنا بتبسيطها لأنه كما نلاحظ فإن R=r ولدينا m2 في الطرفين فنجد :

القوة الناتجة عن الجاذبية F
ثابت الجذب العام ويساوي في تقدير النظام القياسي G
كتلة الأرض M
كتلة الجسم الذي نريد قياس قوة الجاذبية عنده مثال القمر الصناعي m
البعد بين الجسمين ( بين مركزيهما ) d
يجب أن تعرف هذا القانون جيدا لكي نستخدمه فيما بعد في ربط الحلقات بين القوة الطاردة المركزية والجاذبية الأرضية.
2- قوة الطرد المركزي
قوة الطرد المركزي هي قوة غير حقيقية ولكن يمكننا القول على أنها ناتجة عن أن الأجسام تميل للسير في خط مستقيم وفي حالة جسم يدور في مسار دائري فهو في كل مرة يميل للخروج عن مساره ولكن القوة الجاذبة المركزية ( في حالة قمر صناعي هي الجاذبية األرضية ) تمنعه عن الخروج وهنا نقول أن الدفع للخارج ال توجد قوة تسببه فهو نتاج عن العطالة الذاتية لألجسام ( السير في خط مستقيم بسرعة ثابتة تسمى العطالة الذاتية ).
ربما الصصورة التالية توضح لكم الأمر بشكل جيد:
ونلاحظ هنا أن هناك ثلاث أشياء تأثر على قوة الطرد المركزي هي نصف قطر الدوران وسرعة الجسم وكتلته وهي ثلاث متغيرات فقط تدخل في بناء معادلة قوة الطرد المركزي وهي كالتالي:
قوة الطرد المركزي F
كتلة الجسم m
سرعة الجسم v
نصف قطر الدوران R
3- قوة الإحتكاك وقوة الإحتكاك في الفضاء
قوة الإحتكاك هي قوة معاكسة للقوة المحركة وتعمل على تقليل سرعة الأجسام، وهي ناتجة عن تلامس بين جسمين، على الأرض يعمل الهواء على إعاقة حركة الطائرات من خلال الإحتكاك بهيكل الطائرة وفي نفس الوقت هو عنصر مهم في طيرانها لأنه بدون إحتكاك بالهواء لا يمكن للطائرة أن تطير. وعلي تقديم ملاحظة هنا وهي أن القوة المحركة هي قوة تجعل الشيء يتحرك قد تكون دفعا أوليا أو محركا أو دافعات نفاثة.
في الفضاء يوجد الفراغ، ما نعني بالفراغ هو عدم وجود غازات ولكن لكي نتحدث بشكل دقيقة يوجد القليل جدا من الغازات حيث نسبتها تقترب من الصفر ولكن عموما ولأننا نحب التقريب فإننا نقول أنه لا يوجد غازات في الفضاء لأنها بالطبع هي مأثرة على المدى الطويل جدا، فننطلق من هذا ونقول أنه لا يوجد إحتكاك في الفضاء وهذا شيء مهم جدا لأن الإحتكاك كما قلت سابقا يمنع على تقليل سرعة الأجسام وإعاقة مسارها وهو ما يجعلنا نحتاج لقوة محركة في كل مرة لدفع الأجسام ولكن في الفضاء لا يوجد هذا فأنت إذا دفعت الجسم لن يتوقف عن الدوران وهو ما تحدثت عنه في قصة المدفع أين عندما قذفنا القذيفة وبدون وجود إحتكاك لم تتوقف عن إكمال مسارها ( نحن نسمى الغازات بالهواء بالشكل العام ) لذلك نقول أن الهواء على الأرض هو ما يسبب الإحتكاك مع الأجسام الطائرة وبكل ما يحمله ذلك الهواء فنحن إما سنستفيد منه مثال في إقلاع الطائرة بشكل إيجابي أو سيأثر علينا بشكل سلبي في حالة أننا نريد رمي شيء في الفضاء ولا نريده أن يتوقف لذلك في الفضاء لا يوجد هواء وهذا ما يدفعنا إلى أن نقول أنه لا يوجد إحتكاك.
4- قانون نيوتن الثاني
بداية سأقول أنه لن أستخدم قانون نيوتن بالشكل الكامل ولكن سأستخدمه لأوضح شيئا واحدا فقط بسيطا ولكن للمعرفة فإن قانون نيوتن الثاني ينص على أنه "إذا أثرت قوة أو مجموعة قوة على جسم فإنها تكسبه تسارعا يتناسب طرديا مع محصلة القوى المؤثرة عليه وعكسيا مع كتلته" ويكتب :
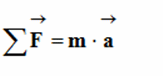 الفائدة من هذا القانون في دراستنا هو لمعرفة أن القمر الصناعي عندما نتركه في سرعة إبتدائية لن يتوقف عن الدوران أي أن هدفنا هو أن نرى فقط القوى المؤثرة على القمر الصناعي تتمثل في القوة المحركة فقط وهو شيء مهم جدا في دراستنا. ولننظر الآن لمحصلة القوى المأثرة على قمر صناعي في دورانه.
الفائدة من هذا القانون في دراستنا هو لمعرفة أن القمر الصناعي عندما نتركه في سرعة إبتدائية لن يتوقف عن الدوران أي أن هدفنا هو أن نرى فقط القوى المؤثرة على القمر الصناعي تتمثل في القوة المحركة فقط وهو شيء مهم جدا في دراستنا. ولننظر الآن لمحصلة القوى المأثرة على قمر صناعي في دورانه.
نعتبر أولا أن :
القوة المحركة للقمر الصناعي F
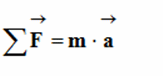
نعتبر أولا أن :
القوة المحركة للقمر الصناعي F
القوة المعيقة للقمر الصناعي أو قوة اإلحتكاك B
قوة الطرد المركزي A
قوة الجاذبية الأرضية P
فنكتب الآن محصلة القوى المؤثرة على القمر الصناعي من خلال قانون نيوتن الثاني:
من أجل أن يسير القمر إنطلاقا من سرعة إبتدائية وبدون توقف نحن نحتاج إلى أن تبقى فقط القوة المحركة، وهذا يكون من خلال أن الإحتكاك يجب أن يكون معدوما
وكذلك بالنسبة للجاذبية الأرضية وقوة الطرد المركزي. في الفضاء الإحتكاك معدوم وسبق توضيح ذلك ويتبقى لنا فقط الجاذبية وقوة الطرد المركزي التي لا يمكن أن يكونا معدومين ولكن كما نلاحظ فهما متعاكسين في الإتجاه إذن يمكن أن يكونا متساويين ومنه ولأنهما متعاكسين نستطيع الوصول إلى إعدامهما معا ومنه ستبقى لنا فقط القوة المحركة. إذن هدفنا التالي هو إيجاد شرط يكون تكون فيه الجاذبية والقوة الطاردة المركزية متساويتين ومنه نستطيع تثبيت هذا الشرط للحصول على قمر صناعي يسير بدون دوافع.
5- قوة الدفع وقوة الجاذبية
في المحور السابق أنهيت بأنه علينا أن نجعل قوة الدفع المركزي وقوة الجاذبية متسوايتين ولذلك من أجل أن يسير القمر الصناعي بشكل لا نهائي بدون محرك فقط من خلال سرعة إبتدائية وقلت تحديدا أنه علينا البحث عن شرط نتحكم به لنحقق الفكرة. إذن ما أقصده بالتساوي هو هذه المتطابقة :
من خلال هذه المعادلة يمكننا معرفة السرعة التي يجب أن ندفع بها القمر الصناعي لكي يسير بدون دافعات بعد ذلك وهي :
إذن فقط من خلال معرفة ثابت الجذب العام وكتلة الأرض والمسافة بين مركز الأرض ومركز القمر الصناعي ستجد السرعة التي يجب أن تدفع بها القمر الصناعي لكي يعمل بدون محركات. ملاحظة جديدة وهي أن هناك من يستخدم متوسط كثافة الأرض في المعادلة كبديل عن كتلة الأرض وسيصل لمعادلة ذات عنصرين هي نصف قطر الأرض وبعض الثوابت المعروفة لذلك قد تختلف بعض الشيء المعادلات ولكن الفكرة نفسها وهي أنه بإمكاننا تشغيل قمر صناعي بدون محركات ولكن هل هذا يعني أننا نتخلى عن المحركات بشكل كامل؟
هذا غير صحيح لأنه أحيانا في مناطق تتغير جاذبية الأرض وقد تأثر على القمر الصناعي جاذبية الشمس والقمر لذلك علينا أن نقوم بتشغيل الدافعات لتصحيح المسار، فالمعادلة السابقة هي معادلة نظرية ولكنها تقدم لنا صورة مميزة على إمكانية المعادلات الرياضية في بناء إبتكارات جديدة كما علي أن أذكر أن الأقمار الصناعية المنخفضة أو بالأصح ذات المدارات المنخفضة تحتاج لتصحيح دائما بسبب عامل إحتكاكه القليل مع الغلاف الجوي وأيضا أنبه إلى شيء آخر أحيانا الهوائيات الموجودة بالقمر الصناعي لا تعمل إلا إذا كانت متجهة نحو مركز التحكم في الأرض لذلك على القمر الصناعي أن يصحح وضعه من خلال الدفع وانت تتساؤل من أين ستأتيه الطاقة وسأقول لك بأن الطاقة الشمسية هي أحد الحلول لفعل هذا .
هذا غير صحيح لأنه أحيانا في مناطق تتغير جاذبية الأرض وقد تأثر على القمر الصناعي جاذبية الشمس والقمر لذلك علينا أن نقوم بتشغيل الدافعات لتصحيح المسار، فالمعادلة السابقة هي معادلة نظرية ولكنها تقدم لنا صورة مميزة على إمكانية المعادلات الرياضية في بناء إبتكارات جديدة كما علي أن أذكر أن الأقمار الصناعية المنخفضة أو بالأصح ذات المدارات المنخفضة تحتاج لتصحيح دائما بسبب عامل إحتكاكه القليل مع الغلاف الجوي وأيضا أنبه إلى شيء آخر أحيانا الهوائيات الموجودة بالقمر الصناعي لا تعمل إلا إذا كانت متجهة نحو مركز التحكم في الأرض لذلك على القمر الصناعي أن يصحح وضعه من خلال الدفع وانت تتساؤل من أين ستأتيه الطاقة وسأقول لك بأن الطاقة الشمسية هي أحد الحلول لفعل هذا .
الوسوم :
#حركة_الاقمار_الصناعية #كيف_يعمل_القمر_الصناعي #كيف_يتحرك_القمر_الصناعي












مقال اكثر من رائع بارك الله فيك
ردحذفافضل مقال اقراه حول الاقمار الصناعية كفيت ووفيت ياغالي
ردحذف